マヤ暦 英 Maya calendar
マヤ人は時の記録に没頭したといわれるように，碑文には必ずといっていいほど日付の表記がある。その暦は，ちょうど西暦がキリストの誕生を起点とするように，ある日を起点（暦元，紀元前 3114 年 9 月 6 日）として，そこからどれくらい経ったかを記す暦である。ひとつの日について，いろいろな方法で述べた暦，つまり，いろいろな周期をもつ暦が積み合わさってできた暦でもあるので，一見複雑に見えるかもしれない。
数字
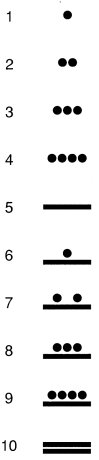
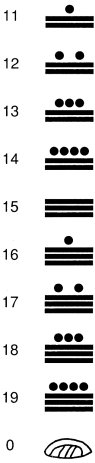
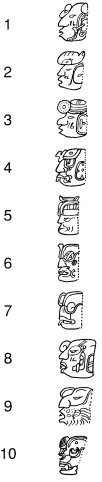
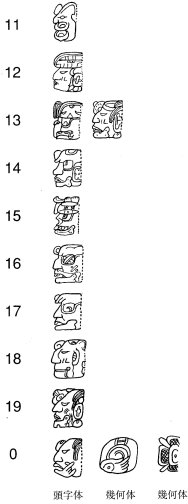
数字は点と棒で示す。点は 1，棒は 5 を表す。ただし，「0」だけは下記の文字を用いる。また，数字は頭字体（頭または横顔を描いた字体）でも示される。頭字体では，13 以降は 10 をあらわすあご骨が付く。文字で表す場合は，バクトゥンとかトゥンといった「期間の文字」（後述）を用いるため，20 以上の数を表す文字は必要ない。
| 点と棒 | 頭字体 | |||
 |
 |
 |
 |
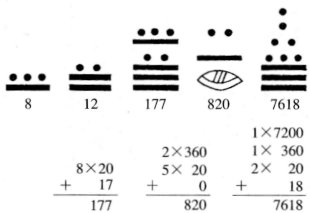
点と棒による表記の場合は，位置によって位取りをするので，0 が必要になる。位取りは下から上に上がる。マヤの数字の数え方は 20 進数である，ただし，下から 3 つ目の位は他の位と違い，18 までしかないため，この位の単位は 360 （20 × 18）に，4 つ目の位の単位は 72000 （20 × 18 × 20）となる。
| 数字の表し方 |
 |
全身像で表された数字
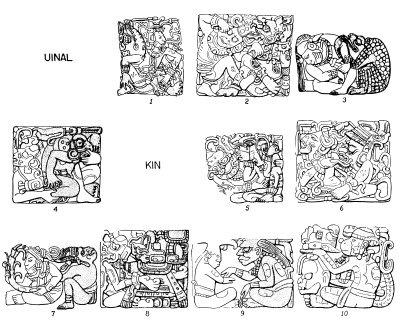
マヤ文字の傑作ともいえる文字が全身像で表される文字である。全身像の数は，左側に添える係数と，右側に後述する長期暦で用いる「期間の文字」と結合している。「期間の文字」バクトゥンを表す 5 種類の文字は 9 バクトゥンを，同じく文字カトゥンは順に，17 カトゥン，16 カトゥン，15 カトゥン，16 カトゥン，17 カトゥン，10 カトゥンを，同様にトゥンは 10 トゥン，15，5，13，1，14 を，文字ウィナルは 0 ウィナル0，0，4 を，文字キンは 0 キン，0，0，17，８，16 を表す。（→ Thompson, Fig. 28, 29）
| 全身像で表された数字 |
 |
 |
暦を表す文字
260 日暦と 365 日暦
マヤ暦は，暦元の日から途切れることなく数える暦であり，時の直線性をよく表している。しかし日が繰り返し，季節が繰り返すように，暦には循環する暦も必要になる。それをマヤ人は 260 日で 1 周期の暦と，365 日で 1 周期の暦を使って表した。下記の図は，→ ランダの『ユカタン事物記』に記された 260 日暦と 365 日暦の文字である。
| 260 日暦 | 365 日暦 | |
| 
|
260 日暦
260 日暦は，1 から 13 までの数字と 20 の日が順次組み合わさってできる暦である。20 日周期と 13 日周期がそれぞれ独立に変動していき，260 日を数える。たとえば，日本の，十干と十二支を組み合わせた 60 を周期とする干支のと同じような数え方である。
260 日暦は，1 イミシュ，2 イック，3 アクバル，4 カン，5 チュクチェアン，6 キミ，7 アニック，8 ラマット，9 ムルック，10 オック，11 チェエン，12 エップと数え，13 ペンの次は，数字は 13 までしかないので 1 に戻る。1 イシュ，2 メン，3 キップ，4 カーバン，5 エツナッぷ，6 カワック，7 アハウで，20 日の日は最後までくる。次の日は最初に戻って，イミシュだが，数字のほうは 7 の次なので 8 イミシュとなる。9 イック，10 アクバルという順で，13 の数字と 20 の日が組み合わさってできる 260 日が 1 周期の暦である。259 日目は 12 カワック，260 日目が 13 アハウで，この周期の最後になる。
| 260 日暦の碑文と絵文書の書体例 | ||
 |
 |
365 日暦
365 日暦（Haab）は，20 日が一月となる月が 18 に，不吉な日とされるワヤップとも呼ばれている 5 日 がついてできる 365 日が 1 周期の暦（ほぼ太陽暦）である。一月は 20 日からなる。そして， 各一日の表し方は月の名の前に 0 から 19 までの数字が順について表される。
たとえば，0 ポープ，1 ホープ，2 ポープ，3 ポープ，…… 18 ポープ，19 ポープとポープ月が過ぎると，次の月ウォが始まる。0 ウォ，1 ウォ，2 ウォ…… 18 ウォ，19 ウォと，同じように 20 日の月になる。こうして，シップ，ソッツ，セック，シュル，ヤシュキン，モル，チェン，ヤシュ，サック，ケフ，マック，カンキン，ムアン，パシュ，カヤップ，クムクとそれぞれが 20 日の月が過ぎると，最後に 5 日しかないワヤップがくる。0 ワヤップ，1 ワヤップ，2 ワヤップ，3 ワヤップ，4 ワヤップとなると 365 日が経ったことになる。次は最初に元って 0 ポープの日となる。
| 365 日の碑文と絵文書の書体例 | ||
 |
 |
| 着座の文字 |
 |
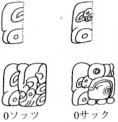なお，うるう年はないので，古代エジプト暦と同様に季節と月日はどんどんずれていく。気候の観点からはそれでも問題はないだろうが，チチェン・イッツア遺跡の神殿で春秋分に大蛇（ククルカン）が舞い降りる仕掛けを見ても，1 年の長さを強く意識していたことがうかがわれる。このククルカン神殿の階段は 91 段 × 4 面 + 頂上の 1 段 ＝ 365 段で，Haab 年の日数に一致する。（ →暦 Wiki）
260 日暦と 365 日暦の組合せによる日の表記
260 日暦と 365 日暦は独立にカウントされ，組み合わせて日付を表す。干支と日付を並べて書くようなものだが，むしろ年が記されない。
 |
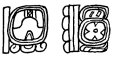5 キップ 14 ヤシュキン 数字は点・棒が用いられる。 |
 |
9 マニック 0 カヤップ 9 は点・棒で表される。0 は即位を表す表語文字と同じ。カヤップという月が着座するという意味になる。 |
 |
12 アハウ 8 ケプ アハウは頭字体で，ケプは上部が幾何体で下部が頭字体で表される。 |
カレンダー・ラウンド
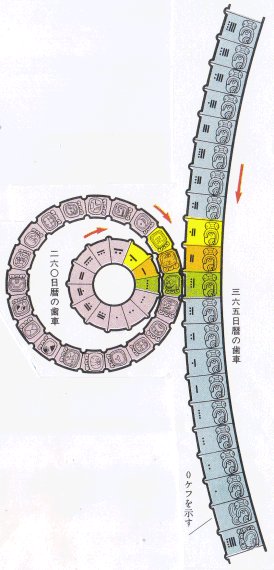260 日暦と 365 日暦が組になって 1 つの単位を作る暦は，260 と 365 の最小公倍数の 18890 日で 1 周期となる。この暦は果てしなく巡ることから，カレンダー・ラウンドと呼ばれている。（→ 八杉 1979）
260 日暦と 365 日暦の組合せにはあるきまりがある。右図に示したように，2 つの暦を歯車にたとえてみる。365 日暦が 1 回転したときには，260 日暦はすでに 1 回転し，さらに 105 日進んでいる。よって，365 日たつごとに，260 日暦の日はもとの日から 5 日ずつ先にずれていくし，また 13 ある日の係数は 1 つずつふえていくことになる。365 日暦が 4 回まわると，つまり，マヤ暦で 4 年たつと，260 日暦の日のほうはおなじ日に戻る。しかし，係数は 4 ふえる。
260 日暦は，1 から 13 までの数字と 20 の文字が順次組み合わさり，1 回りが 260 日となる暦であった。365 日暦は，0 から 19 までの数字が 18 ある月にそれぞれついて 360 日となるものに，5 日の不吉な日とされるジャップがついてできる暦である。
260 日暦を日，365 日暦を月とみれば，われわれの現在使っている暦の月日に相当するといえる。たとえは，1 月 1 日というのを，マヤ暦では 4 アハウ 8 クムラというのである。
時を記す方法
長期暦
時を定める基本となる暦は，長期暦とよばれる暦である。マヤ人は西暦と同じように，はじめの日（暦元）を決めて，そこから日を数えていく絶対暦ともいえる暦表記方法をもっていた。長期暦は 5 つの期間，または時の単位，バクトゥン，カトゥン，トゥン，ウィナル，キンからなる。キンとは，ユカテコ語で，日または太陽を意味する。トゥンを除き 20 進法に従っている。これらの単位を日に換算すると次のようになる。
| バクトゥン | 20 × 18 × 20 × 20 | = | 144000 日 | （= 20 カトゥン） |
| カトゥン | 20 × 18 × 20 | = | 7200 日 | （= 20 トゥン） |
| トゥン | 20 × 18 | = | 360 日 | （= 18 ウィナル） |
| ウィナル | = | 20 日 | （= 20 キン） | |
| キン | = | 1 日 |
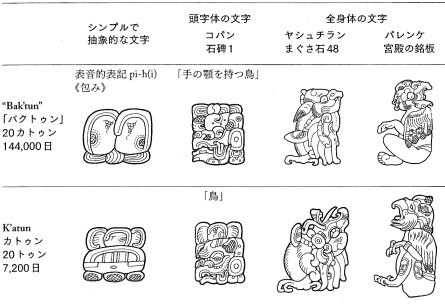
| 期間を表す文字の書体例 （→ マイケル・D.コウ） |
 |
 |
下記の例はすべて 9 バクトゥンという期間を表す文字を，3 字体，幾何体・頭字体・全身体で書いたものである。9 という数字は，最初の 2 例では，点と棒で，3 番目では頭字体で，全身体の 9 は，頭字体の特徴であるひげがあごのところに書かれている。また，頭字体の額のところにある緑を表す文字が全身体では頭の後ろに載っている。これらの特徴から他の数字と区別される。
暦元の日
長期暦は，上記の 5 つの単位の数字を順に並べて暦を記す。マヤ人は前の周期の終わりの日である 13 バクトゥン，0 カトゥン，0 トゥン，0 ウィナル，0 キン，4 アハウ，8 クムクの日 13.0.0.0.0 を暦元の日（西暦紀元前 3114 年 9 月 6 日）と考えた。次の日は，次の周期の初めの日とし，マヤ暦で表すと 0.0.0.0.1 5 イミシュ 9 クムクとなる。なお，この周期の終わり 13.0.0.0.0 は，2012 年 12 月 21 日にあたるため，人類の終焉説が流布した一時期があった。
イニシャル･シリーズ
石碑の最初には，長期暦といわれる暦表記がある。石碑の最初にでてくるのでイニシャル・シリーズと呼ばれている。その上に，他の文字と比べて大きい文字がある。導入文字という（後述）。中央に可変要素をもつが，365 日暦の月と関係し，月が変わるごとに変わるので，月の守護神と考えられている。つぎにバクトゥンに始まる期間を表す文字が係数をともない現われる。文字は一般に，左から右へ，2 列を対に上から下へと読まれる。
その次にはふつう 260 年暦の日付がくるが，対になる 365 日暦との間に数字を添えた一塊の文字群があり，これを「補足シリーズ」と呼ぶ。260 年暦の日の文字の直後に書かれる文字が G と，それを修飾する文字 E である。 Gは 9 つの異なった文字からなり，夜の 9 王の名，または称号をあらわすものと考えられている。9 日が 1 周期の暦である。
| G の 9 つの文字 |
 |
補足シリーズの G と F 以外の文字は，月シリーズと呼ばれている文字群が続く。マヤ人は災いをもたらす日食や月食を畏れ，月の状態の計算はきわめて重要であった。その結果，イニシャル・シリーズの中で長期暦の後に続く文字の多くが月に関係していた。次に主な内容を挙げる。
| 文字 D を表す文字の書体例 |
 |
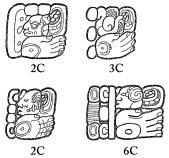
| 文字 C を表す文字の書体例 |
 |
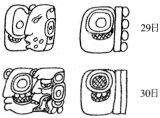
| A の文字 4 例 |
 |
「キリグアの石碑 E」とバレンケの「十字の神殿」における，時を記す方法について事例を挙げる。（→ 八杉 1979）
 |
続いて，補助シリーズの夜の王 G9 〈欄 B6〉 ，月のシリーズの文字 E・D 〈欄 B7〉，文字 A は〈欄 B9〉で 30 日の月（左の要素が 20 を右の頭字体は数 10 の頭字体）であることを示している。〈欄 A10〉では 365日暦の 18 クムクを表している。
2 つの例からわかるように，「キリグアの石碑 E」の場合，数字は丸と棒で，期間の文字は頭字体で表されているのに対し，バレンケの「十字の神殿」の場合は，数字は頭字体で，期間の文字は幾何体で表されている。
導入文字と月の守護神
| 導入文字 |
 |
| 月の守護神の書体例 |
 |
 |
テキスト例
下図はヤシュチランのイニシャルシリーズと呼ばれるものである。AB 列に暦を表わす文字が出てくる。AB1 の大きな文字はここから暦が始まることを表す導入文字である。
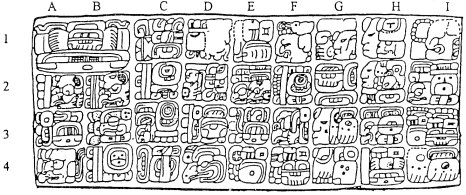
まとめると，9.16.1.0.0 11 アハウ 8 セック（西暦 752 年 4 月 27 日）となる。
A2： 9 バクトゥン（点 4 つと棒 1 つで 9，バクトゥンの頭字体） B2： 16 カトゥン（点 1 つと棒 3 つで 16，カトゥンの頭字体） A3： 1 トゥン（点 1 つで 1，トゥンの幾何体，間にある文字は助数詞 te を表す） B3： 0 ウィナル（0 を表す幾何体，ウィナルの頭字体，その下に音声補助府） A4： 0 キン（0 を表す幾何体，キンの頭字体，その右に音声補助府） B4： 11 アハウ（点 1 つと棒 2 つで 11，アハウの幾何体） D3： 365 日暦，8 セック（点 3 つと棒 1 つで 8，セックの文字間にある文字は助数詞 te を表す）
関連リンク
マヤ暦 | Maya calendar- FAMSI Date Conversion
注
- 八杉佳穂（1979）「マヤ文字解読の試み」『季刊民族学』3 (4)
- -- （2003）『マヤ文字を解く』（中央公論新社）
- -- （2005）『マヤ文字を書いてみよう読んでみよう』（白水社）
- マイケル・D.コウ, マーク・ヴァン・ストーン著; 猪俣健監修; 武井摩利訳（2007）『マヤ文字解読辞典』（創元社）
- ランダ [著] ; 林屋永吉 訳 ; 増田義郎 注 『ユカタン事物記』（大航海時代叢書 第2期 13 岩波書店, 1982）
- Thompson, J. Eric S. (1971) Maya Hieroglyphic Wriing; Introducion (Univerity of Oklahoma Press)
